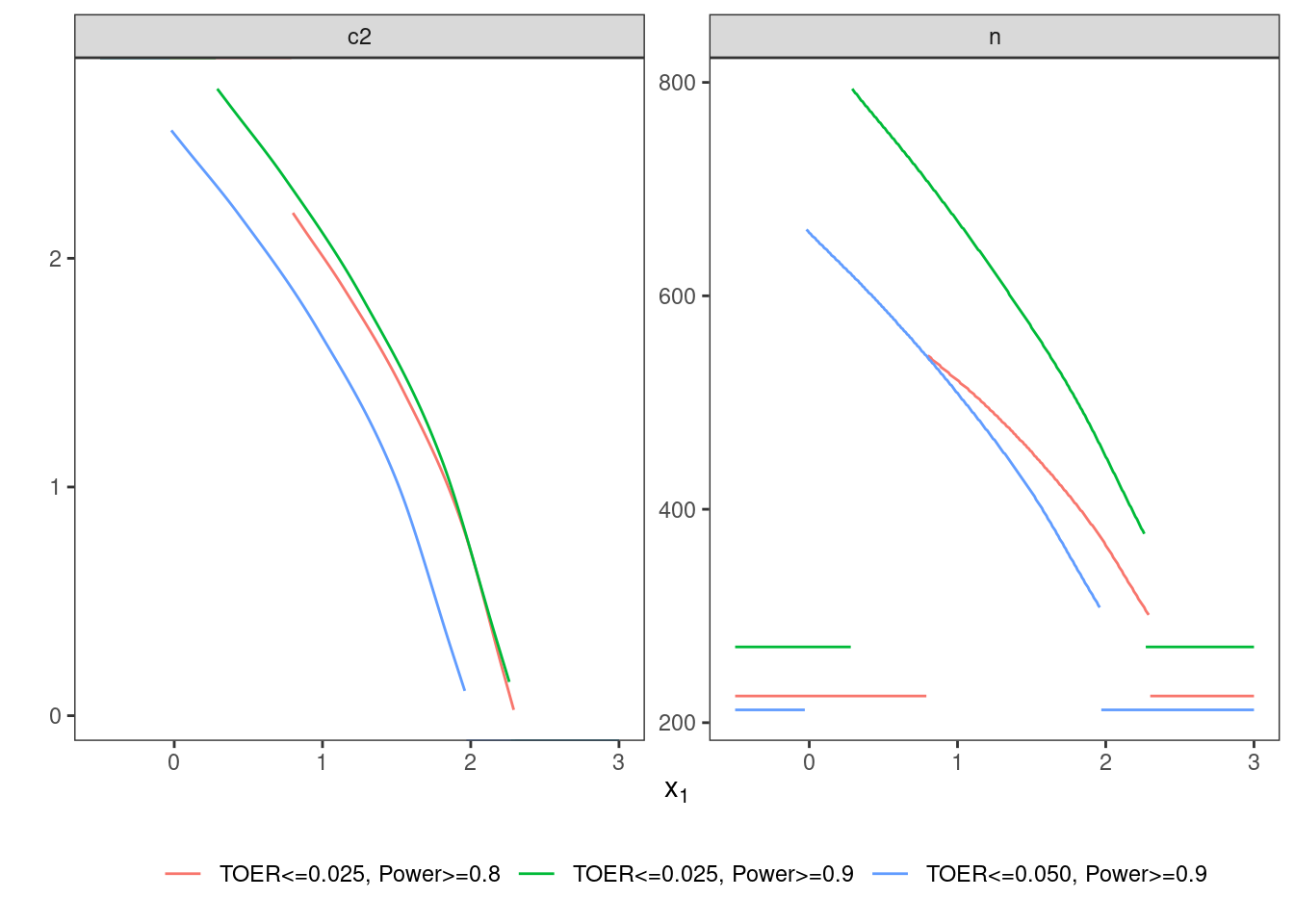
5 Scenario IV: smaller effect, point prior
5.1 Details
In this scenario, we return to point priors as investigated in
Scenario I.
The main goal is to validate adoptr’s sensitivity with regard to
the assumed effect size and the constraints on power and type one error rate.
Therefore, we still assume a two-armed trial with normally distributed outcomes. The assumed effect size under the alternative is \(\delta = 0.2\) in this setting. Type one error rate is protected at \(2.5\%\) and the power should be at least \(80\%\). We will vary these values in the variants IV.2 and IV.3
# data distribution and hypotheses
datadist <- Normal(two_armed = TRUE)
H_0 <- PointMassPrior(.0, 1)
prior <- PointMassPrior(.2, 1)
# constraints
alpha <- 0.025
min_power <- 0.8
toer_cnstr <- Power(datadist, H_0) <= alpha
pow_cnstr <- Power(datadist, prior) >= min_power5.2 Variant IV-1: Minimizing Expected Sample Size under Point Prior
5.2.1 Objective
Expected sample size under the alternative point prior \(\delta = 0.2\) is minimized.
ess <- ExpectedSampleSize(datadist, prior)5.2.3 Initial Design
For this example, the optimal one-stage, group-sequential, and generic
two-stage designs are computed.
The initial design that is used as starting value of optimization is defined
as a group-sequential design by the package rpact that fulfills
type one error rate and power constraints in the case of group-sequential and
two-stage design.
The initial one-stage design is chosen heuristically.
The order of integration is set to \(5\).
order <- 5L
tbl_designs <- tibble(
type = c("one-stage", "group-sequential", "two-stage"),
initial = list(
OneStageDesign(500, 2.0),
rpact_design(datadist, 0.2, 0.025, 0.8, TRUE, order),
TwoStageDesign(rpact_design(datadist, 0.2, 0.025, 0.8, TRUE, order))) )5.2.4 Optimization
tbl_designs <- tbl_designs %>%
mutate(
optimal = purrr::map(initial, ~minimize(
ess,
subject_to(
toer_cnstr,
pow_cnstr
),
initial_design = .,
opts = opts)) )5.2.5 Test Cases
Firstly, it is checked whether the maximum number of iterations was not exceeded in all three cases.
tbl_designs %>%
transmute(
type,
iterations = purrr::map_int(tbl_designs$optimal,
~.$nloptr_return$iterations) ) %>%
{print(.); .} %>%
{testthat::expect_true(all(.$iterations < opts$maxeval))}## # A tibble: 3 × 2
## type iterations
## <chr> <int>
## 1 one-stage 20
## 2 group-sequential 739
## 3 two-stage 2196Now, the constraints on type one error rate and power are tested via simulation.
tbl_designs %>%
transmute(
type,
toer = purrr::map(tbl_designs$optimal,
~sim_pr_reject(.[[1]], .0, datadist)$prob),
power = purrr::map(tbl_designs$optimal,
~sim_pr_reject(.[[1]], .2, datadist)$prob) ) %>%
unnest(., cols = c(toer, power)) %>%
{print(.); .} %>% {
testthat::expect_true(all(.$toer <= alpha * (1 + tol)))
testthat::expect_true(all(.$power >= min_power * (1 - tol))) }## # A tibble: 3 × 3
## type toer power
## <chr> <dbl> <dbl>
## 1 one-stage 0.0251 0.799
## 2 group-sequential 0.0250 0.800
## 3 two-stage 0.0250 0.800Due to increasing degrees of freedom, the expected sample sizes under the
alternative should be ordered as ‘one-stage > group-sequential > two-stage’.
They are evaluated by simulation as well as by evaluate().
tbl_designs %>%
mutate(
ess = map_dbl(optimal,
~evaluate(ess, .$design) ),
ess_sim = map_dbl(optimal,
~sim_n(.$design, .2, datadist)$n ) ) %>%
{print(.); .} %>% {
# sim/evaluate same under alternative?
testthat::expect_equal(.$ess, .$ess_sim,
tolerance = tol_n,
scale = 1)
# monotonicity with respect to degrees of freedom
testthat::expect_true(all(diff(.$ess) < 0)) }## # A tibble: 3 × 5
## type initial optimal ess ess_sim
## <chr> <list> <list> <dbl> <dbl>
## 1 one-stage <OnStgDsg> <adptrOpR [3]> 392 392
## 2 group-sequential <GrpSqntD> <adptrOpR [3]> 324. 323.
## 3 two-stage <TwStgDsg> <adptrOpR [3]> 320. 319.Furthermore, the expected sample size under the alternative of the
optimal group-sequential design should be lower than for the
group-sequential design by rpact that is based on the inverse normal
combination test.
tbl_designs %>%
filter(type == "group-sequential") %>%
{ expect_lte(
evaluate(ess, {.[["optimal"]][[1]]$design}),
evaluate(ess, {.[["initial"]][[1]]})
) }Finally, the \(n_2\) function of the optimal two-stage design is expected to be monotonously decreasing:
expect_true(
all(diff(
# get optimal two-stage design n2 pivots
tbl_designs %>% filter(type == "two-stage") %>%
{.[["optimal"]][[1]]$design@n2_pivots}
) < 0) )5.3 Variant IV-2: Increase Power
5.3.2 Constraints
The minimal required power is increased to \(90\%\).
min_power_2 <- 0.9
pow_cnstr_2 <- Power(datadist, prior) >= min_power_25.3.3 Initial Design
For both flavours with two stages (group-sequential, generic two-stage)
the initial design is created by rpact to fulfill the error rate constraints.
tbl_designs_9 <- tibble(
type = c("one-stage", "group-sequential", "two-stage"),
initial = list(
OneStageDesign(500, 2.0),
rpact_design(datadist, 0.2, 0.025, 0.9, TRUE, order),
TwoStageDesign(rpact_design(datadist, 0.2, 0.025, 0.9, TRUE, order))) )5.3.4 Optimization
tbl_designs_9 <- tbl_designs_9 %>%
mutate(
optimal = purrr::map(initial, ~minimize(
ess,
subject_to(
toer_cnstr,
pow_cnstr_2
),
initial_design = .,
opts = opts)) )5.3.5 Test Cases
We start checking if the maximum number of iterations was not exceeded in all three cases.
tbl_designs_9 %>%
transmute(
type,
iterations = purrr::map_int(tbl_designs_9$optimal,
~.$nloptr_return$iterations) ) %>%
{print(.); .} %>%
{testthat::expect_true(all(.$iterations < opts$maxeval))}## # A tibble: 3 × 2
## type iterations
## <chr> <int>
## 1 one-stage 30
## 2 group-sequential 1172
## 3 two-stage 3025The type one error rate and power constraints are evaluated by simulation.
tbl_designs_9 %>%
transmute(
type,
toer = purrr::map(tbl_designs_9$optimal,
~sim_pr_reject(.[[1]], .0, datadist)$prob),
power = purrr::map(tbl_designs_9$optimal,
~sim_pr_reject(.[[1]], .2, datadist)$prob) ) %>%
unnest(., cols = c(toer, power)) %>%
{print(.); .} %>% {
testthat::expect_true(all(.$toer <= alpha * (1 + tol)))
testthat::expect_true(all(.$power >= min_power_2 * (1 - tol))) }## # A tibble: 3 × 3
## type toer power
## <chr> <dbl> <dbl>
## 1 one-stage 0.0251 0.900
## 2 group-sequential 0.0249 0.900
## 3 two-stage 0.0250 0.900Due to increasing degrees of freedom, the expected sample sizes under the
alternative should be ordered as ‘one-stage > group-sequential > two-stage’.
This is tested by simulation as well as by evaluate().
tbl_designs_9 %>%
mutate(
ess = map_dbl(optimal,
~evaluate(ess, .$design) ),
ess_sim = map_dbl(optimal,
~sim_n(.$design, .2, datadist)$n ) ) %>%
{print(.); .} %>% {
# sim/evaluate same under alternative?
testthat::expect_equal(.$ess, .$ess_sim,
tolerance = tol_n,
scale = 1)
# monotonicity with respect to degrees of freedom
testthat::expect_true(all(diff(.$ess) < 0))
testthat::expect_true(all(diff(.$ess_sim) < 0))}## # A tibble: 3 × 5
## type initial optimal ess ess_sim
## <chr> <list> <list> <dbl> <dbl>
## 1 one-stage <OnStgDsg> <adptrOpR [3]> 525 525
## 2 group-sequential <GrpSqntD> <adptrOpR [3]> 405. 405.
## 3 two-stage <TwStgDsg> <adptrOpR [3]> 397. 397.Comparing with the inverse-normal based group-sequential design created
by rpact, the optimal group-sequential design should show
a lower expected sample size under the point alternative.
tbl_designs_9 %>%
filter(type == "group-sequential") %>%
{ expect_lte(
evaluate(ess, {.[["optimal"]][[1]]$design}),
evaluate(ess, {.[["initial"]][[1]]})
) }Since a point prior is regarded, the \(n_2\) function of the optimal two-stage design is expected to be monotonously decreasing:
expect_true(
all(diff(
# get optimal two-stage design n2 pivots
tbl_designs_9 %>% filter(type == "two-stage") %>%
{.[["optimal"]][[1]]$design@n2_pivots}
) < 0) )5.4 Variant IV-3: Increase Type One Error rate
5.4.1 Objective
As in variants IV.1 and IV-2, expected sample size under the point alternative is minimized.
5.4.2 Constraints
While the power is still lower bounded by \(90\%\) as in variant II, the maximal type one error rate is increased to \(5\%\).
alpha_2 <- .05
toer_cnstr_2 <- Power(datadist, H_0) <= alpha_25.4.3 Initial Design
Again, a design computed by means of the package rpact to fulfill
the updated error rate constraints is applied as initial design for the
optimal group-sequential and generic two-stage designs.
tbl_designs_5 <- tibble(
type = c("one-stage", "group-sequential", "two-stage"),
initial = list(
OneStageDesign(500, 2.0),
rpact_design(datadist, 0.2, 0.05, 0.9, TRUE, order),
TwoStageDesign(rpact_design(datadist, 0.2, 0.05, 0.9, TRUE, order))) )5.4.4 Optimization
tbl_designs_5 <- tbl_designs_5 %>%
mutate(
optimal = purrr::map(initial, ~minimize(
ess,
subject_to(
toer_cnstr_2,
pow_cnstr_2
),
initial_design = .,
opts = opts)) )5.4.5 Test Cases
The convergence of the optimization algorithm is tested by checking if the maximum number of iterations was not exceeded.
tbl_designs_5 %>%
transmute(
type,
iterations = purrr::map_int(tbl_designs_5$optimal,
~.$nloptr_return$iterations) ) %>%
{print(.); .} %>%
{testthat::expect_true(all(.$iterations < opts$maxeval))}## # A tibble: 3 × 2
## type iterations
## <chr> <int>
## 1 one-stage 27
## 2 group-sequential 1183
## 3 two-stage 1925By simulation, the constraints on the error rates (type one error and power) are tested.
tbl_designs_5 %>%
transmute(
type,
toer = purrr::map(tbl_designs_5$optimal,
~sim_pr_reject(.[[1]], .0, datadist)$prob),
power = purrr::map(tbl_designs_5$optimal,
~sim_pr_reject(.[[1]], .2, datadist)$prob) ) %>%
unnest(., cols = c(toer, power)) %>%
{print(.); .} %>% {
testthat::expect_true(all(.$toer <= alpha_2 * (1 + tol)))
testthat::expect_true(all(.$power >= min_power_2 * (1 - tol))) }## # A tibble: 3 × 3
## type toer power
## <chr> <dbl> <dbl>
## 1 one-stage 0.0502 0.900
## 2 group-sequential 0.0500 0.900
## 3 two-stage 0.0502 0.900Due to increasing degrees of freedom, the expected sample sizes under the
alternative should be ordered as ‘one-stage > group-sequential > two-stage’.
They are tested by simulation as well as by calling evaluate().
tbl_designs_5 %>%
mutate(
ess = map_dbl(optimal,
~evaluate(ess, .$design) ),
ess_sim = map_dbl(optimal,
~sim_n(.$design, .2, datadist)$n ) ) %>%
{print(.); .} %>% {
# sim/evaluate same under alternative?
testthat::expect_equal(.$ess, .$ess_sim,
tolerance = tol_n,
scale = 1)
# monotonicity with respect to degrees of freedom
testthat::expect_true(all(diff(.$ess) < 0)) }## # A tibble: 3 × 5
## type initial optimal ess ess_sim
## <chr> <list> <list> <dbl> <dbl>
## 1 one-stage <OnStgDsg> <adptrOpR [3]> 428 428
## 2 group-sequential <GrpSqntD> <adptrOpR [3]> 325. 325.
## 3 two-stage <TwStgDsg> <adptrOpR [3]> 319. 319.The expected sample size under the alternative that was used as objective criterion
of the optimal group-sequential design should be lower than for the
group-sequential design by rpact that is based on the inverse normal
combination test.
tbl_designs_5 %>%
filter(type == "group-sequential") %>%
{ expect_lte(
evaluate(ess, {.[["optimal"]][[1]]$design}),
evaluate(ess, {.[["initial"]][[1]]})
) }Also in this variant, the \(n_2\) function of the optimal two-stage design is expected to be monotonously decreasing:
expect_true(
all(diff(
# get optimal two-stage design n2 pivots
tbl_designs_5 %>% filter(type == "two-stage") %>%
{.[["optimal"]][[1]]$design@n2_pivots}
) < 0) )