(Un)conditional Scores in adoptr
There are two fundamental ways of scoring a two-stage design: First, one may assess the performance before observing any data, i.e., at the planning stage. Classical examples for such scores would be power, type-one-error rate, or expected sample size. There is, however, a second perspective. After observing the stage-one outcome, one might be inclined to consider conditional properties of a design. The most prominent example being conditional power (probability to reject the null under the alternative given stage-one outcome). We consider the following example design
design <- TwoStageDesign(
n1 = 100,
c1f = .0,
c1e = 2.0,
n2_pivots = rep(150, 5),
c2_pivots = sapply(1 + adoptr:::GaussLegendreRule(5)$nodes, function(x) -x + 2)
)
plot(design)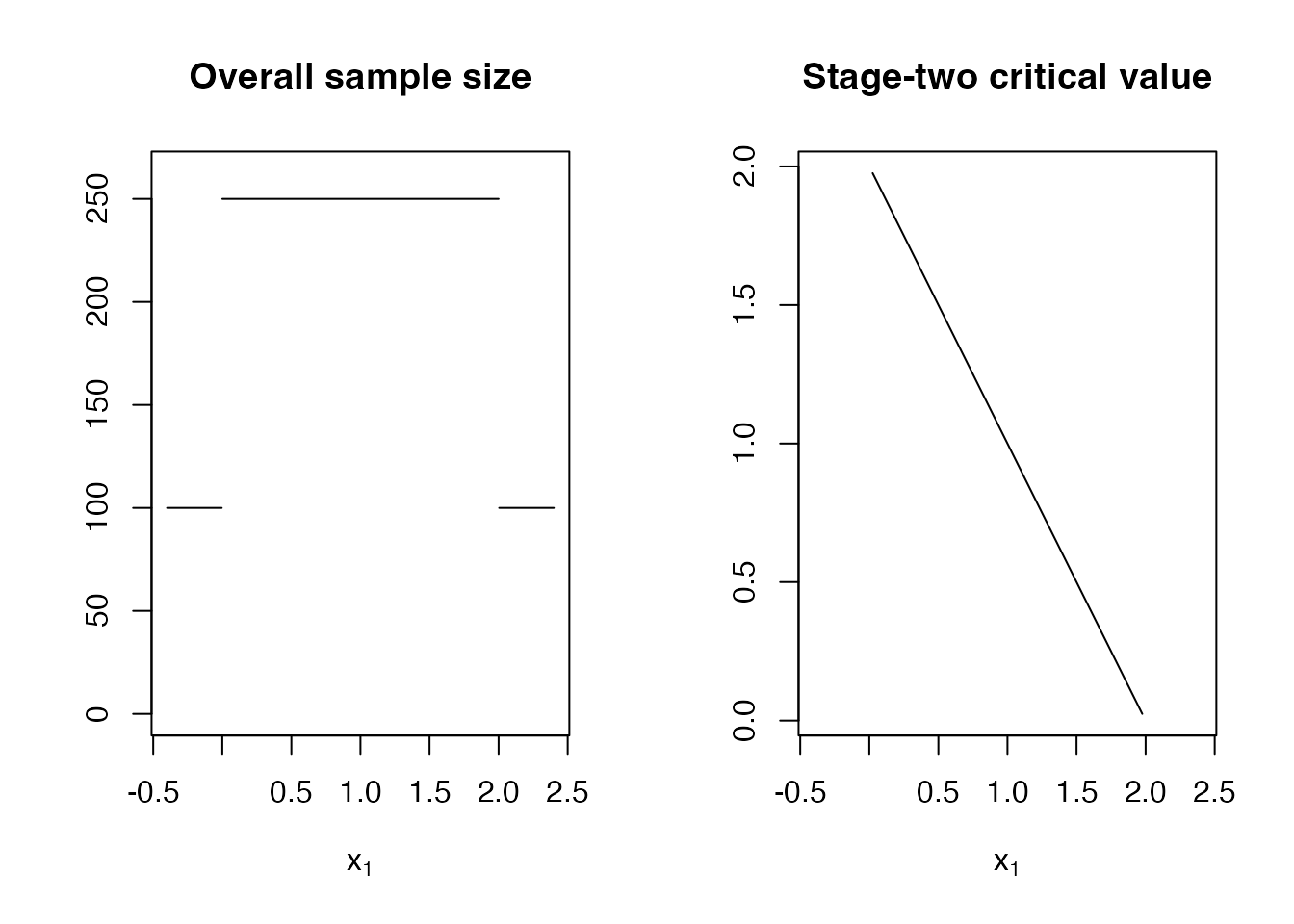
In adoptr, scores are instances of their respective score class. The
most important ones are: ConditionalScore,
UnconditionalScore, and IntegralScore. An
object of class ConditionalScore can evaluate a design for
a particular stage-one outcome. A ConditionalScore is a
function \(s(\mathcal{D}, x_1)\)
evaluating a design \(\mathcal{D}\) at
a stage-one outcome \(X_1 = x_1\). Some
conditional scores might depend on the data distribution (conditional
power) others do not (conditional sample size). Conditional score
evaluation is completely vectorized:
uniform_prior <- ContinuousPrior(
function(x) numeric(length(x)) + 1/.2,
support = c(.3, .5)
)
cp <- ConditionalPower(Normal(), uniform_prior)
css <- ConditionalSampleSize()
x1 <- c(0, .5, 1)
evaluate(cp, design, x1)
#> [1] 0.8312538 0.9303985 0.9772962
evaluate(css, design, x1)
#> [1] 250 250 250Conditional scores can also be plotted directly for a given design by
including them in the plot() call.
plot(design, "Conditional Power" = cp)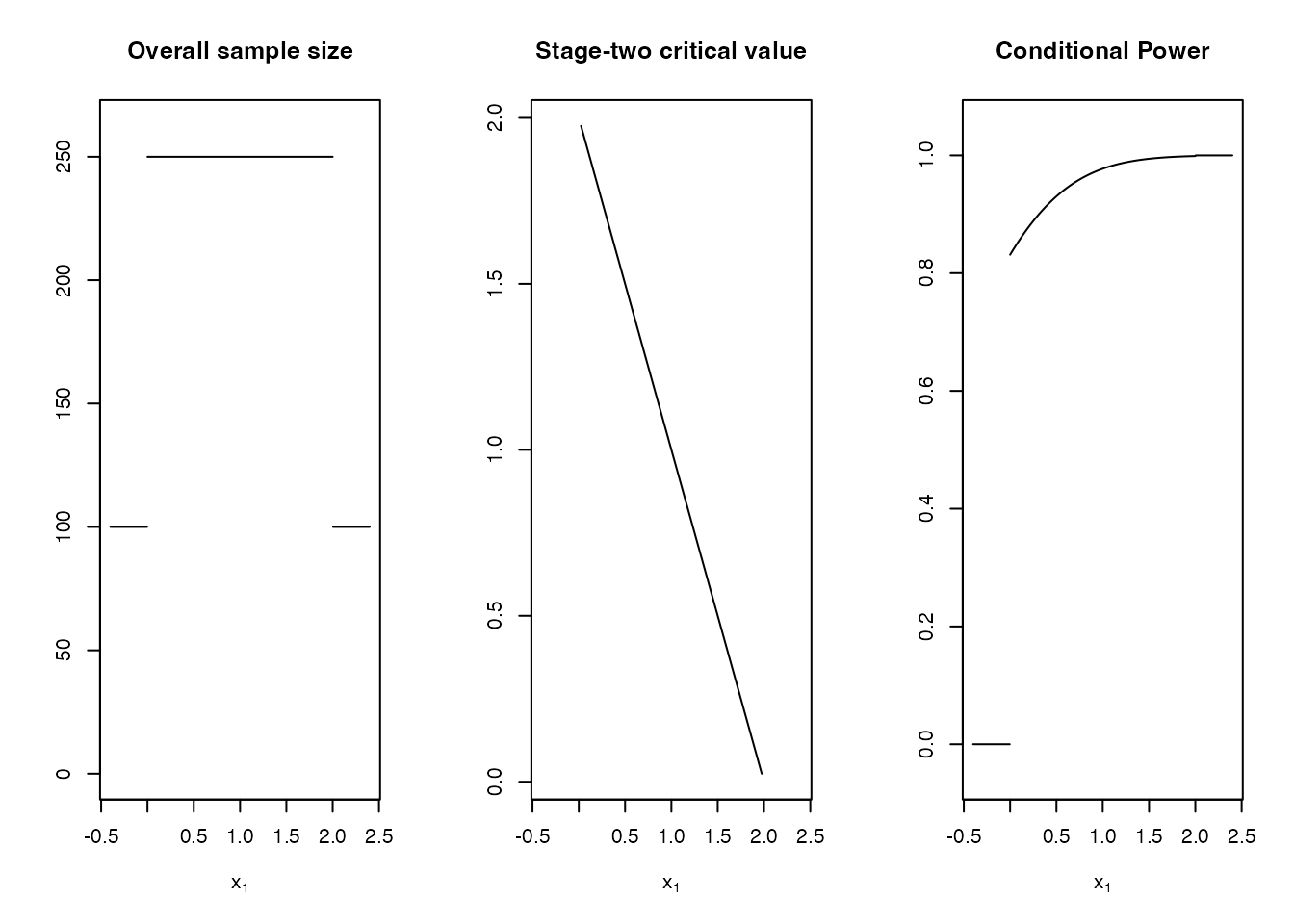
Any conditional score can be integrated with respect to a prior and
data distribution to obtain an unconditional score. Note that for
conditional scores which depend on a specification of these
distributions (e.g., conditional power) these arguments must be
consistent! The resulting score is of class IntegralScore,
a specific subclass of UnconditionalScore and evaluates
designs independent of a particular \(x_1\), i.e., unconditionally
Power at a point alternative can be obtained by forming the expected value with respect to a point prior. For convenience, we include a constructor for power directly, e.g., both variants are equivalent and give power at \(0.4\).
power1 <- expected(
ConditionalPower(Normal(), PointMassPrior(.4, 1.0)),
Normal(), PointMassPrior(.4, 1.0)
)
power2 <- Power(Normal(), PointMassPrior(.4, 1.0))
evaluate(power1, design)
#> [1] 0.9967857
evaluate(power2, design)
#> [1] 0.9967857Similarly, ExpectedSampleSize is a shorthand constructor
for expected conditional sample size, i.e., the overall expected sample
size:
ess1 <- expected(ConditionalSampleSize(), Normal(), uniform_prior)
ess2 <- ExpectedSampleSize(Normal(), uniform_prior)
evaluate(ess1, design)
#> [1] 134.9135
evaluate(ess2, design)
#> [1] 134.9135Conditional Constraints
The same syntax for constraint specification as for unconditional constraints (power etc.) can be used for conditional scores (e.g. conditional power) as well. Currently, these constraints apply to the continuation area only. E.g.,
cp >= 0.7
#> -Pr[x2>=c2(x1)|x1] (x1) <= -0.7 for x1 in [c1f,c1e]imposes a constraint on the minimal conditional power upon continuation. Inter-score comparisons are also supported, e.g.
cp >= ConditionalPower(Normal(), PointMassPrior(0, 1))
#> Pr[x2>=c2(x1)|x1] - Pr[x2>=c2(x1)|x1] (x1) <= 0 for x1 in [c1f,c1e]Would enforce that conditional power is always larger than conditional error.